Chains and rings

After hours spent looking in my books and searching the internet, I came to the conclusion that chemists talk about chains and rings without explaining what they mean. The only definition I found so far, viz. that of Gold Book, is specific for polymers and seems to be too complex to be used in general chemical nomenclature:

The whole or part of a macromolecule, an oligomer molecule or a block, comprising a linear or branched sequence of constitutional units between two boundary constitutional units, each of which may be either an end-group, a branch point or an otherwise-designated characteristic feature of the macromolecule.

(1)

On the other hand, general dictionary definitions of (chemical) chains are not precise enough. For example, Collins English Dictionary defines chain (chemistry) as

two or more atoms or groups bonded together so that the configuration of the resulting molecule, ion, or radical resembles a chain.

(2)

whereas Merriam-Webster says that it is

a number of atoms or chemical groups united like links in a chain.

(3)

So chain (chemistry) is like a chain. Is it?

Well, there is a class of macromolecules called catenanes that consist of at least two interlocked macrocycles (i.e. rings!) and so are, indeed, like a real chain.

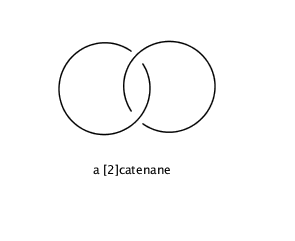
Maybe we don’t need definitions. “You know it when you see it”, as they say. Of course, this “it” refers to a graphical representation of the structure in question. It seems obvious that the structure (a) is a chain while (b) is indubitably a ring. But what about (c)?

(a)	(b)	(c)

hexane cyclohexane bisabolane (trivial) 1-(1,5-dimethylhexyl)-4-methylcyclohexane (substitutive) 1-methyl-4-(6-methylheptan-2-yl)cyclohexane (substitutive)

When we talk about chains and rings, do we refer to the molecular entities or parts thereof? The example (c) above seems to suggest the latter, viz. that (c) contains the chain (a) and the ring (b).

What’s the minimum number of atoms in a structure to be considered a chain? In my opinion, three. (Also, three is the minimum number of atoms in a ring.) Consider this: a real chain consists of at least two connected links. One link is not a chain; neither are two loose links. Likewise, chain in chemical sense should contain at least two adjacent chemical bonds. One dioxygen molecule, O=O, is not a chain; two dioxygen molecules still are not a chain. The ozone molecule, O=O=O, is a chain. Is the structure (d) a chain then?

(d)

H2S hydrogen sulfide (binary) dihydridosulfur (additive) sulfane (parent hydride)

Why, H–S–H looks like a chain to me: three atoms, two adjacent bonds. But I already hear people protesting. Inorganic chemists are likely to think of SH₂ as a mononuclear structure, while for organic chemists it is a parent hydride; the hydrogens are not considered a part of a skeleton. Typical graphical representations of organic structures do not show any hydrogens bound to carbon atoms, except for terminal ones maybe.

Yet the hydrogens are there. So, the structure (e) is a chain and the structure (f) is a ring.

(e)	(f)

H3+ trihydrogen(1+) B2H6 diborane(6)

If structural formula can tell us whether the molecular entity in question contains chain(s) or ring(s), it only seems logical to define chains and rings on the basis of structural formulae. It surely must have been done already by those working in chemical graph theory. I just can’t find those definitions spelled out in black and white.

Let’s think of a structural formula as a graph in a hope that we can take all what we need from graph theory. So...

• A (undirected simple) graph G consists of a set V of vertices (aka nodes) and a set E of pairs of vertices called edges; thus G = (V, E).
• A molecular graph is a (undirected simple) graph whose vertices V correspond to the atoms and edges E correspond to bonds.
• The order of a graph is its number of vertices |V|; therefore, the order of a molecular graph is the same as the number of atoms^*.
• The size of a graph is its number of edges |E|, i.e. number of bonds.
• The degree (or valency) of a vertex is its number of incident edges; accordingly, the degree of an atom in a molecular graph is the number of distinct bonds attached to it.
• Two edges are adjacent if they share a common vertex.
• Two vertices are adjacent if they share a common edge.
• A subgraph of a graph G is another graph G′ formed from a subset of the vertices and edges of G.
• A walk is a sequence of edges (i.e. bonds) which joins a sequence of vertices (i.e. atoms).
• A trail is a walk in which all edges (i.e. bonds) are distinct.
• A path is a trail in which all vertices (i.e. atoms) are distinct.
• A cycle is a trail in which the only repeated vertices are the first and last vertices.
• A cycle graph is a graph that consists of a single cycle.
• An acyclic graph is a graph without cycles.
• A connected graph is an undirected graph in which every pair of vertices is joined by a path.
• A tree is a connected acyclic graph.
• A unicyclic graph or 1-tree is a connected graph that contains a single cycle.

Diestel [1, pp. 6—7] defines path and cycle as follows:

• A path from vertex x₀ to vertex x_k is a non-empty graph P^k = (V,E) of the form
  V = {x₀, x₁, ..., x_k}; E = {x₀x₁, x₁x₂, ..., x_k−1x_k}
  where the x_i are all distinct.
• The number of edges of a path is its length.

Hence the length k of the path P^k is equal to its size |E|; its order |V| = k+1.

• A cycle is the graph C^k = P^k−1 + x_k−1x₀, where k≥3.
• The length of a cycle is its number of edges (or vertices).

Thus the length k of the cycle C^k is equal to its size |E| and its order |V|.

So we can define a chain (in chemical sense) as

a path consisting of at least two adjacent edges (bonds) linking at least three vertices (atoms), or Pk where k≥2.

(4)

García-Domenech et al. [2] provide an alternative:

End vertices are called terminals, and a tree with two terminals is called a chain.

(5)

Both definitions (4) and (5) imply that the chain is unbranched. Is it so? Let’s come back to hexane (a):

This is a typical representation of unbranched carbon chain. Even so, we know that in reality there are also hydrogen atoms. Here’s how a complete structural formula of hexane looks like:

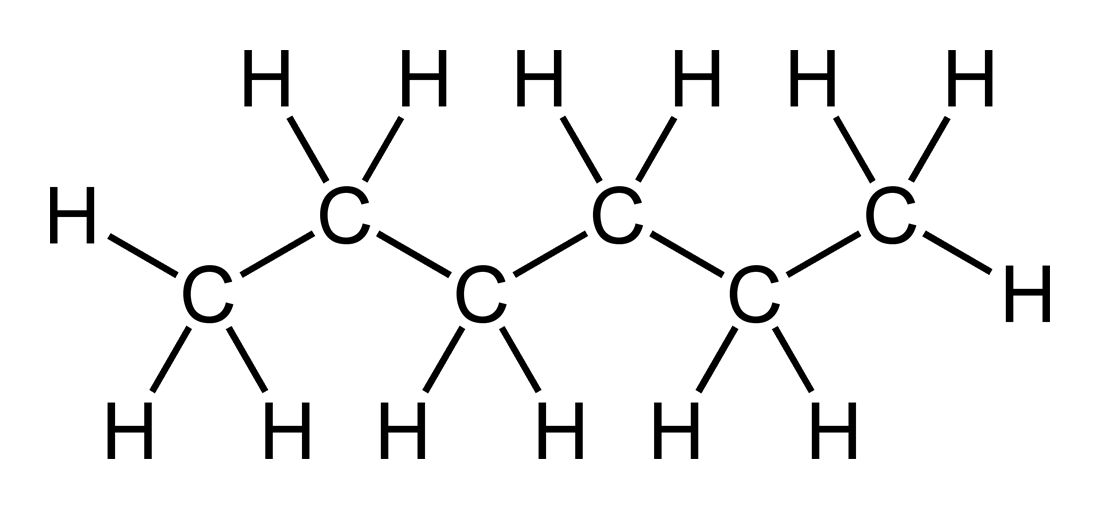
So the whole thing is not a chain but a tree. What shall we do?

Well, we can define a carbon chain or carbochain as a chain in which all vertices are carbon atoms. So for carbon-containing molecules a carbon chain is a subgraph of a molecular graph. We can further expand this definition to all non-hydrogen atoms and call it, say, a hydrogenless chain, although I don’t expect many people to like this name. Alternatively, we can start with hydrogen-depleted, or hydrogen-suppressed, graphs, i.e. the molecular graphs with hydrogen vertices deleted, and then proceed with looking for chains.

Similarly, the complete structure of cyclohexane (b) is not a cycle graph but a 1-tree. We can define a carbocycle as a cycle in which all vertices are carbon atoms; define a hydrogenless cycle as a cycle in which all vertices are atoms other than hydrogen; or look for cycles in hydrogen-depleted graphs. The structure of diborane(6) (f) is also a 1-tree but in this case we cannot ignore hydrogens because then we’ll lose the cycle.

I just noticed that I used the term “unbranched” without defining it. What’s that?

We can define branching point of a graph as a vertex with a degree more than 2. In a molecular graph, that corresponds to an atom connected to more than two other atoms. Once again, organic chemists may want to disregard hydrogens, so we can accordingly modify our definition for carbon chains/hydrogenless chains and so on. Thus, unbranched graph is a graph that has no branching points. Although the definitions (4) and (5) render the phrase “unbranched chain” tautological, it is in wide use.

The beginning and end of the path could be chosen arbitrarily. Consequently, a part P′ of a cycle C could be legitimately considered a chain, provided it consists of at least two adjacent edges:

P′ = (V′,E′)
V′ = {x_i, ..., x_j}; E′ = {x_ix_i+1, ..., x_j−1x_j}
where |E′|≥2.

One could find this useful when talking about macrocycles^†.

Curiously, IUPAC came very close to defining chains and rings in inorganic structures [3]. However, in those recommendations, it is graphs that are defined in terms of chains and rings rather than the other way round. For instance, an acyclic graph is defined as

an unbranched chain of nodes, or two or more unbranched chains of nodes connected to each other without formation of a cyclic structure.

I hope in some future IUPAC recommendations they’ll get that right.

What about “side chain”, a term widely used in polymer science and biochemistry? There are side chains and there are side chains, but all of them imply the existence of “main chain”, or backbone.

In polymer science, the backbone is just the longest chain of the macromolecule and side chains are the branches. Only few polymers, e.g. polyethylene, consist of chains that fit our definition of (unbranched) carbon chain. Other polymers consist of sequences of constitutional units that could be intrinsically branched, like polypropylene, or contain cycles, like polythiophene. The way around this is to “contract” the constitutional units into special types of vertices, called “contraction nodes” [3] or “superatoms” [4]. Then we can still define the chain as

a path consisting of at least two adjacent edges (bonds) linking at least three vertices (either atoms or superatoms).

(4′)

In biopolymers such as nucleic acids or polysaccharides, all constitutional units contain rings, so “contracting” them is really necessary if we want to treat them as chains. In proteins and peptides, it is customary to refer to the sequence –NH–C^α_i–C(O)–NH–C^α_i+1–C(O)– ... as “backbone” and to the groups R_i, R_i+1, etc. attached to C^α atoms as “side chains”, although some of the latter hardly qualify: the side chain of glycine is just a hydrogen atom.

*	Not to be confused with bond order.
†	A note 2 to the Gold Book definition (1) says that “a cyclic macromolecule has no end groups but may nevertheless be regarded as a chain”.

References

1. Diestel, R. Graph Theory (2nd ed.). Springer-Verlag, New York, 2000.
2. García-Domenech, R., Gálvez, J., de Julián-Ortiz, J.V. and Pogliani, L. (2008) Some new trends in chemical graph theory. Chemical Reviews 108, 1127—1169.
3. Fluck, E.O. and Laitinen, R.S. (1997) Nomenclature of inorganic chains and ring compounds (IUPAC Recommendations 1997). Pure and Applied Chemistry 69, 1659—1692.
4. Powell, W.H. (1998) Phane nomenclature Part I: Phane parent names (IUPAC Recommendations 1998). Pure and Applied Chemistry 70, 1513—1545.