Let’s name a simple inorganic chain (a):
 |
| (a) |
|---|
|
The shortest systematic name I can think about is 1,2-dinitrosodioxidane, based on the parent hydride dioxidane (aka hydrogen peroxide). Alternatively, we can emphasise the structure’s symmetry by naming it as a dinuclear entity, bis(nitrosyloxygen)(O—O).
Or we can have a go at it employng yet another type of nomenclature developed for inorganic chains and rings (ICR): 2,5-diazy-1,3,4,6-tetraoxy-[6]catena [1, 2 IR-7.4]. What’s going on here?
After hours spent looking in my books and searching the internet, I came to the conclusion that chemists talk about chains and rings without explaining what they mean. The only definition I found so far, viz. that of Gold Book, is specific for polymers and seems to be too complex to be used in general chemical nomenclature:
The whole or part of a macromolecule, an oligomer molecule or a block, comprising a linear or branched sequence of constitutional units between two boundary constitutional units, each of which may be either an end-group, a branch point or an otherwise-designated characteristic feature of the macromolecule. |
(1) |
On the other hand, general dictionary definitions of (chemical) chains are not precise enough. For example, Collins English Dictionary defines chain (chemistry) as
two or more atoms or groups bonded together so that the configuration of the resulting molecule, ion, or radical resembles a chain. |
(2) |
whereas Merriam-Webster says that it is
a number of atoms or chemical groups united like links in a chain. |
(3) |
So chain (chemistry) is like a chain. Is it?
From The Information: A History, A Theory, A Flood by James Gleick:
It was once thought that a perfect language should have an exact one-to-one correspondence between words and their meanings. There should be no ambiguity, no vagueness, no confusion. Our earthly Babel is a falling off from the lost speech of Eden: a catastrophe and a punishment. “I imagine,” writes the novelist Dexter Palmer, “that the entries of the dictionary that lies on the desk in God’s study must have one-to-one correspondences between the words and their definitions, so that when God sends directives to his angels, they are completely free from ambiguity. Each sentence that He speaks or writes must be perfect, and therefore a miracle.” We know better now. With or without God, there is no perfect language.
Leibniz thought that if natural language could not be perfect, at least the calculus could: a language of symbols rigorously assigned. “All human thoughts might be entirely resolvable into a small number of thoughts considered as primitive.” These could then be combined and dissected mechanically, as it were. “Once this had been done, whoever uses such characters would either never make an error, or, at least, would have the possibility of immediately recognizing his mistakes, by using the simplest of tests.” Gödel ended that dream.
On the contrary, the idea of perfection is contrary to the nature of language. Information theory has helped us understand that — or, if you are a pessimist, forced us to understand it.
Many old jokes are based on the stereotype of mathematicians as impractical freaks (as opposed to, say, chemists). Here’s one from my university days (as told by the lecturer in physical chemistry):
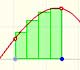
How to calculate the area of this figure? (Draws a squiggly figure on a blackboard.) A mathematician spends three days establishing the nature of the function and two days taking the integral. By the end of the week, the problem is solved. A chemist draws the figure on graph paper, cuts it out and weighs it on an analytical balance. The problem is solved in 10 minutes.
Note that the chemist, apart from being ‘simply’ practical, also provides more direct answer to the question.
I prefer graphics to formulae. If I can’t draw a graph, I won’t grasp a concept. Luckily, there are some great resources on the web. For instance, MatematicasVisuales contains a nice collection of Java applets which elegantly visualise a number of mathematical concepts. Examples range from geometry to probability.
 |  |  |  |  |
This applet illustrates some aspects of the braid theory. Click on ‘draw’, enter a braid word, e.g. BcbACb, and see your braid! The applet also can ‘reduce’, or simplify, the braid diagram, as well as to solve the braid isotopy problem (‘compare’).
 | = |  | = |  |
